Indeks

6. II osa sissejuhatus. Algoritmid.¶

Õpiku esimeses osas tutvustatud programmeerimise mõisted ja vahendid (arvud, sõned, avaldised, muutujad, tingimuslause, korduslause, sisend ja väljund) on teatud nurga alt vaadates kõik, mida programmeerimise kohta on vaja teada. Kui oleksime nõus spetsiifiliste sisend/väljund seadmetega suhtlemise taandama input ja print käskudele, siis hea tahtmise juures saaksime praeguseks tuttavate vahendite abil lahendada suvalise programmeerimisülesande. Samas, kui mõtled päris programmidele, mida sa iga päev kasutad, siis ilmselt nõustud, et midagi jääb veel puudu.

Üks probleem, nagu juba vihjatud, on erinevate spetsiifiliste seadmete juhtimine – ükskõik, kuidas me if-lauseid ja while-tsükleid ei kombineeriks, ei õnnestuks meil arvuti kõlaritesse ühtki piuksu saata ilma vastavaid käske teadmata. Taolistest probleemidest saab harilikult kergesti üle – tuleb vaid järele uurida, millistes moodulites millised funktsioonid soovitud efekti annavad ning lasta programmil neid lihtsalt õigel ajal ja õigete argumentidega välja kutsuda. Mõnede selliste probleemide osas leiab näpunäiteid õpiku lisadest.

Suurem probleem on ülesannetega, mille puhul pole kohe selge, kuidas üldse jõuda sisendist väljundini. Mõnikord tundub ülesande mitteformaalne lahendus küll triviaalne, aga sama lahendust Pythoni programmina vormistades satume raskustesse.

Oletame, et meil on tekstifail, kus igal real on kirjas ühe inimese nimi ja ülesanne on leida sellest loetelust kõige pikem nimi. Kui nimekiri pole väga pikk, siis ülesande käsitsi lahendamiseks piisab faili Notepadis avamisest ja pilguga üle ridade käimisest, võibolla on vaja ka mõned pikemad nimed üksteise alla kopeerida, et nende pikkust täpsemalt võrrelda. Kui üritame sama strateegiat Pythoni programmina kirja panna, siis see tõenäoliselt enam nii lihtne ei tundu, kuigi kõik selleks vajalikud vahendid on meile tuttavad.

Selles õpiku osas keskendumegi programmeerimise sellele osale, mis jääb sisendi ja väljundi vahele, ning uurime standardseid võtteid tüüpiliste programmeerimisprobleemide lahendamiseks.

Selles peatükis astume sammu tagasi ja vaatame üle mõned üldised programmeerimisega seotud küsimused.

Milliseid ülesandeid saab lahendada arvuti abil?
Kas kaks erinevat programmi, mis annavad sama tulemuse, on sama head?
Kuidas keerulistele programmeerimisülesannetele lahendusi leida?

Näited probleemidest¶

Meie igapäevaelus tuleb ette suuri ja väikesi ülesandeid või probleeme. Mõned on lihtsad lahendada, teiste lahendamine pöörab kogu elu pahupidi (nt arst avastab sinu lähedasel ravimatu haiguse). Mõnele ülesandele on olemas standardvastused, teise korral tuleb neid alles hakata otsima, seejuures mõni lahendamata ülesanne tundub huvitavana, mõni mitte. Probleemid varieeruvad oma olemuselt matemaatilistest filosoofilisteni (Mis on elu mõte?).

Vaatame nüüd paari ülesannet, millega võid kokku puutuda. Enne ülesande kommentaari lugemist mõtle, kuidas tuleks sellele ülesandele läheneda ja kas selle lahendamiseks (või lahendamise abistamiseks) saaks kirjutada arvutiprogrammi.

Näide 1. Dokumentideta võõras linnas.¶

Kujutle end võõras linnas välisüliõpilanena. Saabudes ühiselamu juurde avastad, et ühiselamu võti, ID-kaart ja mobiiltelefon on kadunud. Kuidas lahendada olukord?

Kommentaar

Antud ülesande püstitus tekitab palju küsimusi: kuhu need asjad võisid kaduda? Kas need kadusid korraga? Millal need viimati olemas olid? Kas ülikooli ruumidesse pääseb veel sisse, et neid sinna otsima minna? Selliseid küsimusi saab esitada veel ja seetõttu oleks väga raske lahendust üheselt määrata. Me võiksime ju proovida formuleerida kaotatud asjade leidmiseks mingi „retsepti“, aga tõenäoliselt nõuab selle situatsiooni lahendamine ka loovust, st oskust toimida ettenägematus olukorras.

Näide 2. Hundi, kitse ja kapsa üle jõe viimine.¶

Mees peab ületama jõe paadiga, millesse mahub peale ainult üks tema kaaslane. Ta peab üle jõe viima hundi, kitse ja kapsapea. Mees peab tegutsema nii, et samal ajal kui ta ise on paadiga jõel, ei sööks hunt ära kitse ega kits kapsapead.

Leida ülesandele vähemalt üks lahendus.

Kommentaar

Seda ülesannet on arvatavasti oma peaga lihtsam lahendada kui arvutiga, aga võime siiski kujutada ette arvutiprogrammi, mis proovib läbi kõik võimalikud sõidud ja väljastab tulemuseks need, kus lõpuks on kõik tegelased teisel pool jõge ja vahepeal ei jäänud kordagi kits kapsaga ega hunt kitsega omapead.

Samas, me võime seda ülesannet vaadata ka teiselt tasemelt – kui me oleme välja mõelnud sobiva üleveo skeemi, siis võiksime selle põhjal kirjutada programmi robotpaadile, mis tõstab õiged tegelased õigel ajal paati ja viib üle jõe.

Näide 3. Ruut ja ring¶

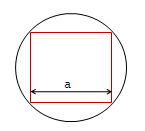
Ringi sisse on joonistatud ruut, mille külje pikkus on a. Leida valem, mis esitab ringi pindala.

Kommentaar

Siin on tegemist täpselt defineeritud geomeetriaülesandega. Peale ülesandest arusaamist on vaja lahendusplaani. On vaja välja selgitada sisend (ristküliku külg), väljund (ringi pindala) ja kasutada sobivat tähistust. Edasi on vaja välja selgitada seos sisendi ja väljundi vahel, mis viib lahenduseni. See võib sisaldada vahepealsete tulemuste arvutamist, nt ristküliku diagonaali arvutamist. On vaja kasutada tasandilise geomeetria põhiteadmisi (antud juhul Pythagorase teoreemi). Täiendame joonist …

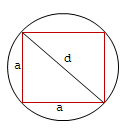
…ja esitame lahenduse kahe sammuna:

$d=\sqrt{a^2+a^2}=\sqrt{2a^2}$ $S=\frac {\pi d^2}{4}= \frac {\pi a^2}{2}$

Nii nagu paadisõidu ülesandes, on ka siin võimalik saadud tulemust ära kasutada teisel tasemel – nimelt ülesandes, mis nõuab valemi rakendamist etteantud sisendandmetega. Selle ülesande lahendamiseks on programmi kirjutamine väga sobiv valik. Samas, valemini jõudmine nõudis loovust ja seega seda osa arvutile me delegeerida ei oleks saanud.

Algoritm¶

Ülalpool toodud näited illustreerivad olukordi, mis tekivad ülesannete lahendamisel. Programmeerimisel tegeleme me probleemidega, mille lahendust saab esitada algoritmina.

Algoritmiks nimetatakse probleemi lahendamiseks vajalikku instruktsioonide hulka, mida mehaaniliselt (st ilma loovust rakendamata) järgides on võimalik jõuda soovitud tulemuseni. Algoritmi kohta öeldakse tihti ka lihtsalt protseduur.

Algoritmil on neli olulist omadust.

Algoritmi iga samm peab olema täpne, st olema ühetähenduslik.
Algoritm peab olema lõplik. Vastasel juhul ei saa me probleemile lahendust.
Algoritm peab olema efektiivne, st ta peab andma probleemile korrektse vastuse.
Algoritm peab olema üldine, st ta peab lahendama ülesande iga eksemplari. Näiteks ringi pindala leidmise algoritm peab sobima kõigi võimalike algandmetega.

Algoritme kasutatakse erinevate elukutsete juures. Näiteks kokk järgib algoritmi, mida nimetatakse retseptiks. Retsept kirjeldab protsessi, mis teisendab rea sammude abil toiduained (sisend) mingiks toiduks (väljund).

Märkus

Sõna algoritm on tuletatud 9. sajandi Pärsia matemaatiku Mohammed al-Khowarizmi nimest. Tema nime ladinapärane kuju on Algorismus.

Kuna algoritmi järgimine ei nõua loovust, siis on algoritme võimalik tõlkida arvuti jaoks arusaadavale kujule (programm) ja seega saab neid vajadusel käivitada arvutil. Sellest vaatenurgast võiksime anda algoritmile ka järgneva, veidi kitsama definitsiooni:

Algoritm on täpselt defineeritud (arvutuslik) protseduur, mis koosneb instruktsioonide hulgast, millele antakse sisendina ette mingi väärtus või väärtuste hulk ja mis leiab väljundiks mingi väärtuse või väärtuste hulga. Teiste sõnadega, algoritm on protseduur, mis võtab andmed ja manipuleerib nendega, järgides ettekirjutatud samme ja leiab otsitavad väärtused.

Mõned ütlevad, et programmeerimine ja algoritmide loomine ongi üks ja sama. Tavapärases kõnepruugis siiski tehakse algoritmil ja programmil vahet: algoritm esitab mingi ülesande lahenduskäiku ilma tehnilistesse detailidesse laskumata (aga siiski ühetähenduslikult), programm on aga tavaliselt mõeldud mingi konkreetse masina (sh virtuaalse masina) juhtimiseks ja võib seetõttu sisaldada nüansse, mis on olulised vaid selle masina kasutamisel.

Kaasaegsetes programmeerimiskeeltes (nt Python) ei ole masina nüanssidele eriti vaja mõelda, seetõttu kasutatakse programmeerimiskeeli juba algoritmide väljatöötamise faasis. Vahel on aga siiski mugavam panna algoritm esialgu kirja kuidagi teisiti, näiteks pseudokoodina (s.o loomuliku keele ja matemaatiliste sümbolite segu) või mingi visuaalse skeemina. Järgnevalt uurimegi lähemalt ühte algoritmide skemaatilise esitamise viisi.

Plokkskeem¶

Üks levinud graafiline notatsioon algoritmide esitamiseks on plokkskeem. Plokkskeemis kasutatakse järgmisi elemente:

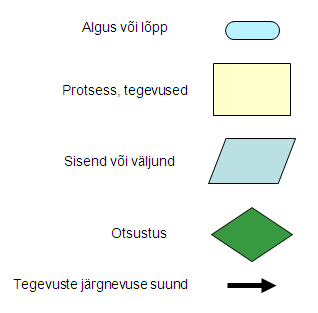
Näide. Kartulisalat.¶

Plokkskeem sobib hästi kasutamiseks ka arvutikaugetes valdkondades. Proovime näiteks selle abil kirjeldada kartulisalati valmistamist:

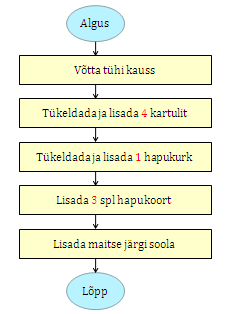
Kui me tahame protsessi täpsemalt kirjeldada, võime lisada kartuleid ühekaupa ja hapukoort ühe lusikatäie kaupa, samal ajal kontrollides, kas vajalik kogus on juba lisatud:

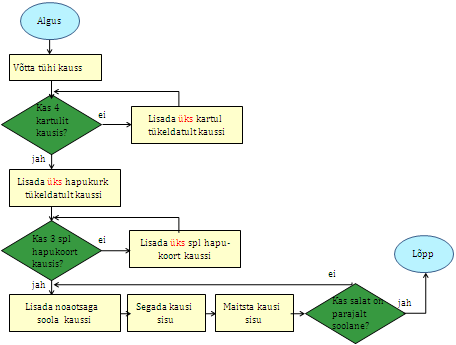
Ka loendamist saame detailsemalt väljendada. Oletame, et me loendame pliiatsi ja paberiga, märkides igal lisamisel paberile ühe kriipsu. Peale kartulite lisamist kustutame kriipsud paberilt, et saaks loendada hapukurkide lisamist:

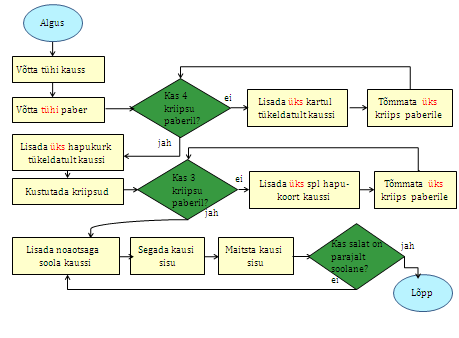
Näide. Kuni kolm sammu ja ümberpöörd.¶

Proovime plokkskeemiga edasi anda ühe Pykkari liikumisskeemi – ta peab astuma kolm sammu, või kui sein tuleb varem vastu, siis seinani, ja seejärel ennast ümber pöörama. Kuna plokkskeem on tavaliselt mõeldud vaid lahendusidee edasiandmiseks, siis ei pea me kasutama täpselt samu käske nagu Pykkari Pythoni moodul ette näeb.

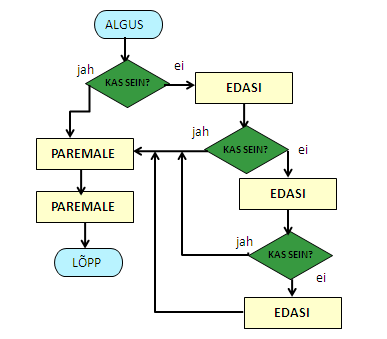
Harjutus. Ring ümber mänguväljaku.¶

Pykkar asub ristkülikukujulise maailma vasakus ülemises nurgas, näoga paremale. Maailma mõõtmed ei ole teada. Joonista plokkskeem, mis paneb Pykkari seina ääred läbi käima. Lõpuks peab ta jõudma esialgsesse positsiooni tagasi.

Märkus

Plokkskeemi võib vabalt käske juurde leiutada – antud ülesandes kuluks arvatavasti ära käsk muutuja defineerimiseks ja suurendamiseks (aga võib ka tõmmata kriipse kujuteldavale paberile, nii nagu kartulisalati näites).

Alaprogrammid plokkskeemis¶

Alamprogramme saab defineerida ka plokkskeemides. Selleks eraldatakse lihtsalt skeemil üks eraldiolev ala alamprogrammi jaoks (näiteks ümbritsetakse kastiga) ning kirjutatakse selle juurde alamprogrammi nimi.

Loome näiteks skeemi, mis paneb Pykkari värvima põrandat põhja-lõuna suunal triibuliseks – alustada tuleks lääneservast, järgmine veerg põrandaruute peab jääma värvimata, ülejärgmine tuleb jälle värvida jne. Maailma mõõtmed pole teada, aga teame, et Pykkar on alguses loodenurgas (NW), näoga lõuna suunas.

Loome kõigepealt alamprogrammid järgmistele tegevustele.

Ühe triibu värvimine kuni seinani.
Tagasitulek sama teed mööda seinani ja lõpuks pööre paremale.

Alamprogramm triip

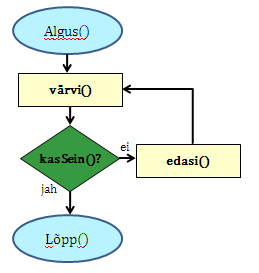
Alamprogramm tagasi

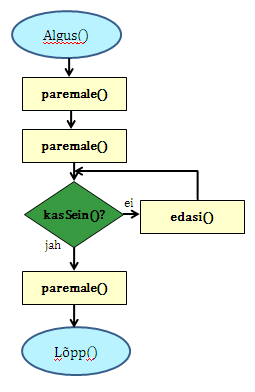
Koostame nüüd plokkskeemi kogu maailma triibuliseks värvimiseks, kasutades juba koostatud protseduure:

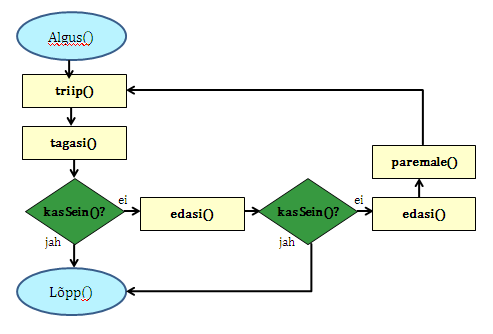
Selline värvimine annab soovitava tulemuse, kuid lahendus sisaldab ülearust tühjalt liikumist lõunast põhja. Koostame nüüd sellise algoritmi, kus Pykkar ei liigu tühjalt, vaid värvib ruudustikku ka liikumisel lõunast põhja. Selleks kasutame juba olemasolevat protseduuri triip ja koostame mugavuse jaoks veel ühe alamprogrammi vasakule pööramiseks:

Alamprogramm vasakule

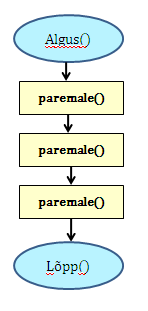
Enne uue triibu värvimist peab Pykkar lõunas pöörama kaks korda vasakule ja põhjas kaks korda paremale. Selle realiseerimiseks võtame appi loenduri l, mille abil saame kindlaks teha, kummale poole on vaja pöörata. Kui loendur jagub kahega, siis on vaja pööramisi vasakule, vastasel juhul paremale. Kogu värvimisprotseduur oleks järgmine:

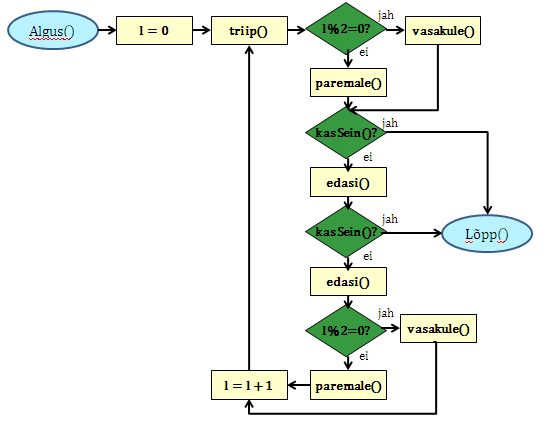
Antud juhul liigub Pykkar ökonoomsemalt, kuid algoritmile vastav plokkskeem on veidi keerulisem.

Käivitatavad plokkskeemid¶

On olemas plokkskeemi joonistamise keskkondi, kus skeemi on võimalik arvutis käivitada justkui programmi. Üks selline asub aadressil http://www.physicsbox.com/indexrobotprogen.html.

Alternatiivsed lahendused¶

Põranda värvimise näite juures andsime kaks alternatiivset lahendust – üks neist oli lihtsam, teine efektiivsem. Algoritmi efektiivsuse ja lihtsuse vahel valimine on programmeerimisel tihti esinev dilemma.

Näide. Pikim sõna.¶

Oletame, et meil on antud fail, mis sisaldab igal real ühte sõna ja me soovime väljastada kõige pikema sõna, või kui sama pikkusega on mitu sõna, siis kõik need, millest pikemaid ei leidu.

Lihtsam lahendus oleks käia fail läbi kaks korda – esimesel korral leiame kõige suurema sõna pikkuse ja teisel korral väljastame kõik sellele pikkusele vastavad sõnad:

fail = open("sonad.txt", encoding="UTF-8")

# selles muutujas hoiame suurimat pikkust, mida oleme kohanud
max_pikkus = 0

while True:
    rida = fail.readline()
    if rida == "":
        break

    sõna = rida.strip()
    if len(sõna) > max_pikkus:
        # leidsime veel pikema sõna
        # uuendame vastavat muutujat
        max_pikkus = len(sõna)

# nüüd on meil muutujas max_pikkus olemas pikima failis esineva sõna pikkus

# sulgeme faili ja avame uuesti
fail.close()
fail = open("sonad.txt", encoding="UTF-8")

# väljastame õige pikkusega sõnad
while True:
    rida = fail.readline()
    if rida == "":
        break

    sõna = rida.strip()
    if len(sõna) == max_pikkus:
        print(sõna)

fail.close()

Sellel lahendusel on kaks probleemi – esiteks, kuna failide lugemine on suhteliselt aeglane toiming, võib selle topelt tegemine mõnikord olla lubamatu ajaraiskamine, teiseks, me pidime kirjutama kaks tsüklit.

Proovime, kas saab paremini. Seekord katsume ühe läbivaatusega pikimad sõnad kohe meelde jätta:

fail = open("sonad.txt", encoding="UTF-8")

# selles muutujas hoiame suurimat pikkust, mida oleme kohanud
max_pikkus = 0

# siin on need sõnad, mis vastavad seni leitud pikimale sõnale
pikad_sõnad = ""

while True:
    rida = fail.readline()
    if rida == "":
        break

    sõna = rida.strip()
    if len(sõna) > max_pikkus:
        # leidsime veel pikema sõna
        # uuendame vastavat muutujat
        max_pikkus = len(sõna)

        # ... ja kirjutame üle seni kogutud pikad sõnad
        pikad_sõnad = sõna + "\n"

    elif len(sõna) == max_pikkus:
        # leidsime sama pika sõna, kui praegune max_pikkus
        # lisame ta leitud sõnade hulka
        pikad_sõnad += sõna + "\n"

# kuvame leitud sõnad (eemaldades ebavajaliku reavahetuse lõpust)
print(pikad_sõnad.strip())

fail.close()

See variant on natuke lühem kui esimene ning ka pisut kiirem, aga kardetavasti vähemalt algajate jaoks raskemini arusaadav. Professionaalsed programmeerijad peavad tihti lisaks programmide korrektsusele jälgima ka etteantud efektiivsuse nõudeid ja samal ajal arvestama enda kaastöötajate tasemega – paratamatult tuleb siin aeg-ajalt teha kompromisse.

Kuidas seda lahendada?¶

Kuna algoritmi koostamine on ülesande lahendamise kõige olulisem osa, siis on seda uuritud ka süstemaatiliselt. Üheks selle ala klassikuks võib lugeda Ungari matemaatikut George Pólyat, kes uuris ülesande lahendamise protsessi lähemalt ja avaldas oma kuulsa raamatu „Kuidas seda lahendada?“. Oma raamatus toob ta välja neli etappi, millega ülesande lahendajal tuleb kokku puutuda. Esitame siinkohal tema kuulsa tsitaadi:

Suur avastus lahendab suure probleemi, kuid väike avastus on olemas iga probleemi lahenduses. Sinu probleem võib olla tagasihoidlik, kuid kui see esitab väljakutse sinu uudishimule ja toob mängu sinu leiutaja omadused, siis on tema lahendamisest selge kasu olemas. Kui sa lahendad seda omaenda vahenditega, võid kogeda pingutust ja nautida avastuse triumfi. Sellised kogemused võivad vastuvõtlikus eas tekitada vajaduse vaimse töö järele ja jätta jälje terveks eluks.

George Pólya selgitab oma raamatus ülesande lahendamise nelja etappi, mida soovitame ka antud kursuse ülesannete korral hoolikalt järgida.

1. Ülesandest arusaamine¶

Mis on otsitav? Mis on antud? Milles seisnevad ülesande tingimused?
Kas tingimusi on võimalik üldse rahuldada? Kas tingimused on otsitava tulemi määramiseks piisavad? Kas nende hulgas on ülearuseid? Kas tingimused on vastuolulised?
Valmista joonis. Võta kasutusele sobiv tähistus.

2. Lahendamise idee ja sellele vastava plaani koostamine¶

Kas tead mõnd teist antud ülesandega seonduvat ülesannet?
Vaatle otsitavat! Püüa meenutada mõnda tuntud ülesannet, milles on sama või sarnane otsitav.
Kas on võimalik seda ülesannet ära kasutada? Kas peab sisse tooma mingi abielemendi, mis võimaldaks varem lahendatud ülesannet ära kasutada?
Kas saab ülesannet teisiti sõnastada? Veel teisiti? Pöördu tagasi definitsiooni juurde.
Kui sa ei suuda antud ülesannet lahendada, siis proovi lahendada kõigepealt mõni temaga seonduv ja võib-olla lihtsam ülesanne. Või üldisem ülesanne? Või erijuht? Või sarnane ülesanne? Jättes osa tingimustest kõrvale, kuivõrd on otsitav siis määratud?
Kas kasutasid kõiki andmeid? Kas kasutasid kõiki tingimusi? Kas arvestasid kõiki ülesandes sisalduvaid mõisteid?

3. Lahendusplaani täitmine¶

Veendu iga sammu õigsuses.

4. Tagasivaade¶

Kas saad kontrollida tulemust? Kas saad kontrollida lahenduskäiku?
Kas saad tulemust teisiti leida?
Kas tulemus või lahenduskäik on kasutatav mõne teise ülesande korral?

Ülesanded¶

1. Põranda värvimine triibuliseks¶

Kirjuta eespool toodud Pykkariga põranda värvimise plokkskeemile vastav Pythoni programm.

2. Takistusest mööda liikumine¶

Pykkar asub ruudustiku suvalisel ruudul. Ruutude arv ei ole teada. Ruudustikul võib olla sirge vahesein, mille otsad ei ulatu ruudustiku servani. Pykkaril on vaja liikuda ruudustiku selle välisseinani, mille poole ta näoga on.

Katseta vähemalt selliste algseisudega:

##########
#        #
#     #  #
#  >  #  #
#     #  #
#        #
##########

##########
#        #
#     #  #
#     #  #
#    >   #
##########

3. Malelaud¶

Joonista plokkskeem ja kirjuta Pythoni programm, mis mõlemad panevad Pykkarit värvima ristkülikukujulist maailma malelaua stiilis ruuduliseks.

4. Efektiivsem kuu nimi¶

Kolmandas peatükis demonstreeriti kahte samaväärset programmi, mis väljastavad etteantud kuu numbrile vastava kuu nime. Leidsime, et teine viis on esimesest parem, kuna teda on lihtsam kirjutada ja lugeda.

Mõlemad näidatud viisid sunnivad Pythonit halvimal juhul tegema kuni 12 võrdlemist (kui sisestatud arv oli 12). Kirjuta veel üks nende kahega samaväärne lahendus, mis saab alati hakkama väiksema arvu võrdlustega.

Vihje

Lahendust on võimalik panna kirja nii, et Python ei pea õige vastuseni jõudmiseks tegema kunagi rohkem kui 4 võrdlust.

Vihje

Siin on parem kasutada ainult tavalisi, üksteise sisse pandud if-else’isid (st mitte kasutada elif-i).

Vihje

Pane tähele, et ühe if-else’i võime paigutada teise if-else’i sisse kahel moel – kas then harusse või else harusse.

Vihje

Mõtle sellele, kuidas sa otsid mingit sõna sõnaraamatust. Kas hakkad sõnastiku algusest lehitsema, kuni jõuad otsitava sõnani, või kasutad mingit kavalamat viisi?

5. Firma statistika¶

Firma hoiab oma klientide nimekirja failis kliendid.txt, kus igal real on ühe kliendi andmed eraldatuna semikooloniga:

AS Kustukumm; Hiie 34, Tartu
FIE Tuudur Tuduur; Kaunase pst 14-11, Tartu
AS Aknapesumasin; Raekoja plats 2-001, Tartu
MTÜ Unihiir; Juutsina küla, Hopi vald, Pärnumaa
...

Pakutavate toodete nimekiri asub failis tooted.txt:

Kärbsepiits; 2 EUR
Paberlennukid (10tk); 1 EUR
Suur ja punane asi; 12 EUR
...

Jooksva aasta müügi nimekiri on failis myyk.txt. Siin on igal real ühe müügitehingu kirjeldus (vabas vormis), semikoolon ja saadud summa eurodes:

mai - arve nr. 12; 1300
mai - arve nr. 13; 23
juuni - Jiiihaaaa! Tuudur võttis kõik kärbsepiitsad ära!; 120
august - arve nr. 15; 12
okt - müüsin meie kaubiku kõrvalistme, et saaks elektri ära maksta; 43
...

Võib eeldada, et tehingu kirjelduses semikoolonit ei esine.

Viimasel kuul välja makstud palgad on failis palgad.txt:

Toomas Tuus; 1300
Eduard Ennatlik; 899
Priit Pätt; 675
Adeele; 400
...

Firma käekäigul silma peal hoidmiseks tuleb nüüd kirjutada programm, mis annab käivitamisel kokkuvõtte mainitud 4 faili hetkesisust. Täpsemalt: ekraanile tuleb näidata

klientide koguarv;
toodete koguarv;
jooksva aasta müügitehingutest saadud summaarne sissetulek;
viimasel kuul väljamakstud palkade summa.

Märkus

See ülesanne on senistest mahukam – võta selle jaoks rohkem aega. Proovi läheneda ülesandele osade kaupa. Vaata, kas erinevate osade vahel on sarnasusi.

Märkus

Sõnest mingi soovitud osa kättesaamise vahendeid on 2. peatükis küll põgusalt mainitud, aga toome nad ka selle ülesande kontekstis ära:

>>> s = "Eduard Ennatlik; 899"
>>> s.find(";")
15
>>> s[15]
';'
>>> i = s.find(";")
>>> s[i]
';'
>>> s[i:]
'; 899'
>>> s[i+1:]
' 899'
>>> int(s[i+1:])
899

Vihje

Selles ülesandes on mõistlik defineerida ja kasutada 2-3 abifunktsiooni.

Vihje

def ridu_failis(failinimi):
    ...
    ridade_arv = 0
    ...
    while ...:
        ...
    ...
    return ridade_arv

...

Vihje

def teise_veeru_summa(failinimi):
    ...
    summa = 0
    ...
    while ...:
        ... arv_peale_semikoolonit(...) ...
        ...
    ...
    return summa

...

Vihje

def arv_peale_semikoolonit(s):
    ...
    return ...

...

>>> arv_peale_semikoolonit("Eduard Ennatlik; 899")
899

6. Üks asi veel¶

Kui eelmises ülesandes mainitud programm sai juba valmis, tuli firmajuhile meelde, et lisaks viimase kuu palkade summale tahab ta näha ka kuu keskmist palka.

Proovi lisada soovitud funktsionaalsus võimalikult lühikese lisakoodiga ilma programmi efektiivsuse pärast muretsemata.

7. Põranda keskkoht¶

Kirjuta programm, mis

küsib kasutaja käest ristkülikukujulise Pykkari maailma mõõtmed ning Pykkari esialgse asukoha ja suuna;
loob mõõtmetele vastava maailma;
paigutab Pykkari nõutud suunaga nõutud positsioonile;
käivitab käsud, mis panevad Pykkarit värvima põranda keskkohta tumedaks. (Pykkari all oleva ruudu saab tumedaks värvida käsuga paint().)

Täpsustused.

Loodud maailma servaruutudes peab olema sein, ülejäänud ruudud peavad olema värvimata põrand.
Kasutaja võib Pykkari suunda anda ilmakaarte tähistega (n, e, s, w, N, E, S, W) või noolekujuliste suunatähistega (^, >, v, <).
Kui maailma põrand laius ja kõrgus on paaritu arv ruute, siis tuleb põranda keskelt värvida täpselt üks ruut. Kui mõlemad mõõtmed on paarisarvud, siis tuleb värvida 4 keskmist ruutu. Kui üks mõõde on paaritu ja teine paaris, siis tuleb värvida 2 ruutu (nii, et värvitud osa jääks täpselt põranda keskele).
Kasutaja käest küsitud sisendit tuleb kontrollida. Programm ei tohi kokku joosta, kui kasutaja sisestab midagi valesti (näiteks sisestab suvalise teksti seal, kus oodatakse täisarvu või sisestab Pykkari algseks positsiooniks sellise, mis ei jää põranda piiridesse). Ebasobiva sisendi korral tuleb küsimist korrata niikaua, kuni sisend sobib.

Näiteks, kui kasutaja ja programmi vahel kujuneb selline dialoog:

Sisesta maailma laius: 10
Sisesta maailma kõrgus: asdf
Vigane sisend! Proovime uuesti ...
Sisesta maailma kõrgus: 7
Sisesta Pykkari positsiooni x-koordinaat: 3
Sisesta Pykkari positsiooni y-koordinaat: 23
Liiga suur! Proovime uuesti ...
Sisesta Pykkari positsiooni y-koordinaat: 0
Liiga väike! Proovime uuesti ...
Sisesta Pykkari positsiooni y-koordinaat: 2
Sisesta Pykkari suund: S

Siis peaks ilmuma kõigepealt selline pilt (siin eeldatakse, et y-koordinaat suureneb ülalt alla):

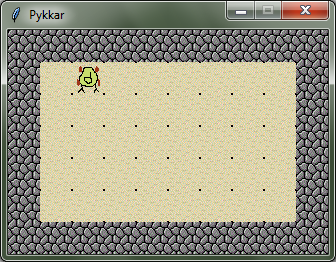
ja Pykkari tegutsemise lõpuks peaks maailm olema selline (Pykkari suund ja asukoht pole tähtis):

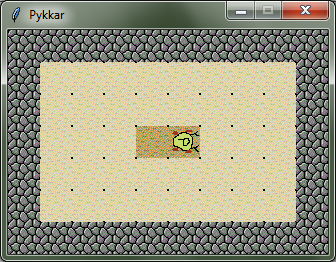
NB!

Kuigi ülesande tekst ühegi alaprogrammi (st funktsiooni) kasutamist ei nõua, on siin palju võimalusi funktsioonide abil koodi selgemaks muuta. Kui märkad oma lahenduses korduvaid sarnaseid koodiplokke, või kui mingi osa koodist läheb väga keeruliseks, siis proovi funktsioonide abil asja parandada.

Ülesande lisa

Proovi lahendada ülesanne nii, et Pykkar ei kasuta kasutaja poolt sisestatud infot maailma mõõtmete kohta, vaid üritab põranda mõõtmed iseseisvalt tuvastada.

Vihje

Ülesande kaks poolt (maailma moodustamine ja selle keskkoha värvimine) on üksteisest kaunis sõltumatud. Kui sa kohe ei oska kasutaja sisendi põhjal maailma moodustada, siis proovi kõigepealt lahendada ülesanne mingi fikseeritud maailmaga.

Vihje

create_world võtab ette lihtsalt ühe sõne ja sõnet on võimalik dünaamiliselt kokku panna.

Vihje

def küsi_kasutajalt_täisarv(küsimus, min, max):
    ...
    ... while ...
    ... input ...
    ... try ...
    ... if ....
    ...

    return ...

Vihje

Erindite püüdmine.

Vihje

Kui jääd dünaamiliselt maailma loomisega hätta, siis kirjuta programmi sisse mingi konkreetne maailm ja proovi lahendada vähemalt värvimise osa.

Vihje

Kui keskkoha värvimine tundub alguses raske, siis lase kõigepealt Pykkaril lihtsalt tuvastada põranda laius ja kõrgus.