Indeks

11. Rekursioon¶

Paljude ülesannete jaoks on olemas väga elegantsed lahendused, kus algse ülesande lahendamiseks lahendatakse kõigepealt väiksem alamülesanne ja seejärel täiendatakse saadud vastust mingil moel. Sarnast skeemi kasutasime korduvalt tsüklite peatükis.

Ilmneb, et taoliste ülesannete puhul on tsüklite asemel võimalik kasutada ka rekursiivseid funktsioone – s.o funktsioone, mis iseennast välja kutsuvad. Tihti on selliselt kirjutatud lahendused selgemad ja lühemad kui tsüklitega kirjutatud lahendused.

Tehniliselt võttes ei õpi sa selles peatükis Pythoni kui programmeerimiskeele kohta midagi uut, kuna Pythoni seisukohast ei erine rekursiivsed funktsioonid tavalistest funktsioonidest. Samas, rekursiivsetest algoritmidest arusaamiseks on vaja vaadata asju pisut teise nurga alt – seetõttu on antud peatükis ülesandeid, mis aitavad rekursiivse mõtteviisiga harjuda.

Prelüüd¶

Kuigi see peatükk alustab lihtsamate rekursiooniskeemidega, siis kõige eredamalt säravad rekursiivsed lahendused ülesannetes, mis tegelevad puukujuliste (st. hargnevate) andmestruktuuridega.

Üks hea näide puukujulisest andmete organiseerimisest on kaustapuu. Näiteks kui sul on Windowsi arvuti, siis sinu peakettal (C: kettal) on hulk faile ja kaustu. Igas kaustas võib omakorda olla hulk faile ja kaustu jne.

Proovime kirjutada funktsiooni, mis kuvab ekraanile kõik etteantud kaustas sisalduvad failid ja alamkaustad. Selle juures on meile abiks funktsioon listdir moodulist os ning funktsioonid join ja isdir moodulist os.path.

import os.path

def kuva_failid(kaust):
    # os.listdir annab etteantud kaustas olevate failide ja kaustade nimed
    # (sõnede listina)
    for nimi in os.listdir(kaust):
        # os.path.join paneb kausta nime ja faili nime
        # kokku täisnimeks (vastavalt platvormi reeglitele kas / või \-ga)
        täisnimi = os.path.join(kaust, nimi)

        # os.path.isdir ütleb, kas tegemist on kaustaga
        if os.path.isdir(täisnimi):
            print("Kaust", täisnimi)
        else:
            print("Fail", täisnimi)

# Asenda Peeter enda kasutajanimega
kuva_failid("C:\\Users\\Peeter") # Mac'i ja Linuxi korral "~/Peeter"

Kui kõik läks hästi, siis kuvas see programmijupp kõik sinu kodukaustas olevad kausta- ja failinimed.

Kuidas aga teha nii, et kuvataks ka alamkaustade ja nende alamkaustade jne. sisu? Proovi programm saada tööle nii, et kuvatakse kõikide, ükskõik kui sügaval olevate kaustade ja failide nimed!

Rekursiivsed funktsioonid¶

Programmeerimises nimetatakse rekursiooniks tavaliselt situatsiooni, kus funktsiooni definitsioonis on kasutatud parasjagu defineeritavat funktsiooni. Kõige lihtsam rekursiivne funktsioon oleks selline:

def f():
    f()

Kui sellist funktsiooni Pythonis välja kutsuda, siis vastavalt definitsioonile tuleb kutsuda seesama funktsioon uuesti välja, see omakorda põhjustab jälle selle funktsiooni väljakutsumise jne. Pythoni puhul lõpeb taoline ahel veateatega, mis ütleb, et alustatud, aga mitte lõpule jõudnud väljakutsete limiit sai täis. (Mõne teise keele puhul võib see protsess lõputult käima jääda.)

Rekursiooni baas ja samm¶

Et rekursioon mingil hetkel lõppeks, peab rekursiivses funktsioonis toimuma hargnemine sõltuvalt funktsiooni argumentidest. Vähemalt üks haru peab olema ilma rekursiivse väljakutseta – seda nimetatakse rekursiooni baasiks. Seda haru, mis kutsub funktsiooni rekursiivselt välja, nimetatakse rekursiooni sammuks.

Rekursiooni samm lahendab tavaliselt ülesande vähendatud koopia e mingi alamülesande (kasutades selleks sedasama funktsiooni) ning koostab saadud tulemuse põhjal terve ülesande lahenduse. Aga kui alamülesanne on piisavalt väike, siis käsitletakse seda baasjuhuna ja vastus antakse ilma rekursiivse väljakutseta.

Näide: Faktoriaal¶

Faktoriaali definitsiooni järgi on 0! = 1. Iga teise naturaalarvu puhul on n! võrdne arvude 1 .. n korrutisega. Nt

4! = 1 × 2 × 3 × 4
5! = 1 × 2 × 3 × 4 × 5

Nagu näha, on 5! arvutus väga sarnane 4! arvutusele – selleks, et arvutada 5! võiksime me arvutada 4! ja korrutada saadud tulemuse 5-ga. Seda asjaolu arvestades on kirjutatud järgnev rekursiivne faktoriaali definitsioon:

def fact(n):
    if n == 0:
        return 1
    else:
        return fact(n-1) * n

Harjutus. Faktoriaali algoritmi analüüs¶

Väärtusta mõttes ülaltoodud definitsiooni järgides avaldis fact(3).
Milline osa antud näites on rekursiooni baas? Milline on samm? Kuidas jõutakse alamülesande lahendusest terve ülesande lahenduseni?
Kuidas käitub antud funktsioon negatiivsete (või reaalarvuliste) argumentide korral? Kuidas võiks seda probleemi lahendada?

Näide: Stardiloendus¶

Rekursiivne funktsioon ei pea alati midagi tagastama:

from time import sleep

def stardiloendus(sekundeid_stardini) :
    if sekundeid_stardini == 0:
        print('Start!')
    else:
        print(sekundeid_stardini)
        sleep(1) # ootab 1 sekundi
        stardiloendus(sekundeid_stardini-1)

Kui antud funktsiooni definitsiooni rahulikult lugeda, siis peaks selle tähendus olema selge – kui me teeme stardiloenduse 0 sekundiga (e baasjuhu korral), siis ei ole vaja midagi loendada, vaid kohe start anda. Vastasel juhul väljastame ekraanile järelejäänud sekundite arvu, ootame ühe sekundi ja alustame ühe sekundi võrra lühemat stardiloendust.

Lisaseletus

Mis toimub Pythoni seisukohast, kui me sellise funktsiooni välja kutsume?

>>> stardiloendus(3)

stardiloendus käivitub argumendiga 3. Kuna see ei võrdu 0-ga, väljastakse väärtus 3 ja stardiloendus kutsutakse välja argumendiga 2.
- stardiloendus käivitub argumendiga 2. Kuna see ei võrdu 0-ga, väljastakse väärtus 2 ja stardiloendus kutsutakse välja argumendiga 1.
  stardiloendus käivitub argumendiga 1. Kuna see ei võrdu 0-ga, väljastakse väärtus 1 ja stardiloendus kutsutakse välja argumendiga 0.
  
  stardiloendus käivitub argumendiga 0 ja kuna see rahuldab if-lause tingimust, siis väljastatakse 'Start!'.
  
  stardiloendus argumendiga 0 lõpetab oma töö.
  
  stardiloendus argumendiga 1 lõpetab oma töö.
- stardiloendus argumendiga 2 lõpetab oma töö.
stardiloendus argumendiga 3 lõpetab oma töö.

Harjutus. Modifitseeritud stardiloendus¶

Muutke eelnevat näidet nii, et peale starti loendatakse veel stardist möödunud sekundeid, st uus_stardiloendus(3) peaks andma sellise väljundi:

3
2
1
Start!
1
2
3

Harjutus. Spiraali joonistamine¶

Kirjuta rekursiivne funktsioon, mis joonistaks kilpkonna abil kandilise spiraali, alustades etteantud küljepikkusest ning vähendades küljepikkust igal ringil mingi väärtuse võrra, kuni see jõuab nulli. (Analoogse ülesande lahendasime ühes varasemas peatükis tsükliga.)

Harjutus. Eukleidese algoritm¶

Eukleidese algoritm leiab kahe naturaalarvu suurima ühisteguri.

Algoritm on järgmine:

Olgu meil naturaalarvud a ja b ning on teada, et a > b.
Kui b = 0, siis on suurim ühistegur a.
Kui ei, siis korda protsessi, võttes uueks a-ks b ja uueks b-ks endiste a ja b jagamisel saadud jääk.

Realiseeri Eukleidese algoritm rekursiivse funktsioonina.

Rekursioon järjenditel¶

Nagu ülalpool mainitud, on rekursiooni põhimõte teha ülesanne pisut väiksemaks alamülesandeks, lahendada see uus ülesanne (sama meetodiga) ning lõpuks jõuda alamülesande lahendusest algse ülesande lahenduseni.

Seda põhimõtet saab hästi rakendada ka järjendite töötlemisel – me korraldame nii, et uueks väiksemaks alamülesandeks on sama toiming listi mingi osa peal (näiteks listi sabal – s.o kõik elemendid peale esimest elementi). Uuri näiteks järjendi elementide loendamise funktsiooni:

def loenda(järjend, element):

    # tühjas järjendis ei saa seda elementi esineda
    # see on rekursiooni baas
    if len(järjend) == 0:
        return 0
    else:
        # rekursiooni samm
        # järjendi päiseks nimetame tema esimest elementi
        päis = järjend[0]
        # sabaks nimetame kõike seda, mis tuleb peale esimest elementi
        saba = järjend[1:]

        # kasutame sama funktsiooni rekursiivselt järjendi sabal ...
        elementide_arv_sabas = loenda(saba, element)

        # ... ja kombineerime saadud tulemuse päisest saadud infoga
        if päis == element:
            return elementide_arv_sabas + 1
        else:
            return elementide_arv_sabas


print(loenda("kukesupp", "u"))
print(loenda("kukesupp", "p"))
print(loenda("kukesupp", "r"))
print(loenda([1,2,3,2,2], 2))
print(loenda([1,2,3,2,2], 8))

Harjutus. Pikkus¶

Kirjuta rekursiivne funktsioon pikkus, mis tagastab argumendina antud järjendi pikkuse (st elementide arvu). Ülesanne tuleks lahendada ilma tsükleid ja len funktsiooni kasutamata.

Hargnev rekursioon e puurekursioon¶

Rekursiivses funktsioonis võib olla mitu rekursiivset väljakutset. Sellist rekursiooniskeemi nimetatakse puurekursiooniks, kuna selle graafilises esituses moodustub funktsiooni väljakutseid tähistavatest nooltest puutaoline kujutis.

Järgnev funktsioon annab Fibonacci arvujada n-nda liikme. Funktsiooni definitsioon põhineb otseselt Fibonacci jada definitsioonil (http://en.wikipedia.org/wiki/Fibonacci_number).

def fib(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fib(n-1) + fib(n-2)

Harjutus. Fraktal¶

Fraktalid on graafilised kujundid, milles kordub sama motiiv üha väiksemal kujul (loodetavasti paistab siit seos rekursiooniga).

Kirjuta rekursiivne funktsioon, mis vastavalt etteantud tasemele joonistab vastava kujundi järgmiselt skeemilt (esimene kujund on tasemega 1, teine tasemega 2 jne):

Selle fraktali joonistamise mitteformaalne juhis: 1 tasemega fraktali joonistamiseks tuleb joonistada kriips; selleks, et joonistada fraktalit tasemega n, tuleb joonistada kriips ja selle kriipsu otsa paremale ja vasakule joonistada vähendatud suurusega fraktalid tasemega n-1.

Vihje

Fraktali joonistamiseks sobib kahe parameetriga funktsioon – üks parameeter määrab, millise taseme juures me parasjagu oleme, teine määrab vaadeldava fraktali osa mõõtmed.

Vihje

Ülesannet on lihtsam lahendada, kui korraldad nii, et funktsiooni lõpus on kilpkonn samas punktis ja sama suunaga nagu funkstiooni väljakutsel.

Näidislahendus

from turtle import *


def fraktal(tase, pikkus):
    if tase >= 1:
        forward(pikkus)
        left(90)
        fraktal(tase-1, pikkus * 0.7)
        right(180)
        fraktal(tase-1, pikkus * 0.7)
        left(90)
        backward(pikkus)



left(90)
fraktal(3, 100)

Alternatiivne lahendus:

def fraktal(tase, pikkus):
    if tase == 1:
        forward(pikkus)
        backward(pikkus)
    else:
        forward(pikkus)
        left(90)
        fraktal(tase-1, pikkus * 0.7)
        right(180)
        fraktal(tase-1, pikkus * 0.7)
        left(90)
        backward(pikkus)

Harjutus. Kuulujutt¶

Keegi laseb lahti kuulujutu, rääkides seda 3 inimesele. Iga tunni jooksul räägivad kõik, kes kuulujuttu juba teavad, selle edasi 3 inimesele, kes seda veel ei teadnud. Mitu inimest teavad kuulujuttu 10 tunni pärast?

Kirjuta rekursiivne funktsioon, mis annab selle ülesande vastuse suvalise tundide arvu korral.

Harjutus. Küülikud¶

Üks XIII sajandi matemaatik tundis huvi küülikute paljunemise vastu. Ta koostas sellise ülesande:

alguses on meil üks äsjasündinud emane ja üks äsjasündinud isane küülik;
küülik saab suguküpseks ühe kuuga (ja ta kasutab oma uut staatust kohe ära);
küüliku tiinusperiood kestab 1 kuu (st küülik poegib 1 kuu pärast viljastamist);
suguküps emane küülik poegib iga kuu järel ja sünnitab igal korral ühe emase ning ühe isase küüliku;
oletame, et küülikud ei sure iial;
mitu paari küülikuid on meil 12 kuu pärast?

Kirjuta üldisem funktsioon, mis annab vastuse suvalise arvu kuude kohta.

Näide: Argumentideta rekursioon¶

Enamasti käib rekursioon muutuja järgi, mida edastatakse funktsiooni argumendina. Kui lõpetamistingimus on esitatud muul moel, võib rekursioon toimuda ka ilma väärtusi edastamata. Järgmine funktsioon laseb kasutajal arvata mündivisete tulemusi, kuni ta mõne neist õigesti arvab:

from random import choice

def mäng() :
    münt = choice(['kull', 'kiri'])
    arvamus = input("Arva, kas kull või kiri: ")

    if (münt == arvamus) :
       print("Arvasid õigesti!")
    else:
       print("Proovi veelkord")
       mäng()

mäng()

Rekursiivsed andmestruktuurid¶

Eelmises peatükis vaatasime, kuidas järjendeid üksteise sisse pannes luua keerulisemaid andmestruktuure. Selle juures aga arvestasime alati, mitu taset meie andmestruktuurides on.

Alati pole tasemete arvu võimalik ette teada – näiteks failisüsteemi puhul pole kaustade sügavus süsteemi poolt (otseselt) piiratud. Ilmneb, et rekursioon sobib ideaalselt taoliste andmestruktuuride töötlemiseks.

Vaatame kõigepealt ühte näiteprogrammi, mis liidab kokku kõik antud mitmemõõtmelises järjendis olevad arvud, olenemata sellest, mitme mõõtmega on tegemist:

def liida(järjend):
    summa = 0
    for element in järjend:
        if isinstance(element, list):
            summa += liida(element)
        else:
            summa += element
    return summa

print(liida([1, [2, 3], [[[[4, 5], 6]]], 7, 8]))
print(liida([1, 2, 3, 4, 5, 6, 7, 8]))

Kuna me ei teadnud, kas mingil tasemel on meil järjendis veel järjendeid või tulevad juba arvud, siis kasutasime funktsiooni isinstance elemendi andmetüübi testimiseks.

Kõrvalepõige

Erinevates teooriates käsitletakse tihti ka naturaalarve rekursiivsete andmestruktuuridena. Meile tuttavaid vahendeid kasutades võiksime esimesi naturaalarve esitada näiteks järgnevalt:

0 — []
1 — [[]]
2 — [[[]]]
jne.

Kas oskaksid kirjutada funktsiooni taoliselt esitatud naturaalarvude liitmiseks?

Ülesanded¶

0. Kaustade läbimine¶

Kirjuta lõpuni peatüki prelüüdis alustatud programm!

1. Kaustad ja järjendid¶

Kirjuta funktsioon, mis etteantud kaustanime põhjal moodustab ja tagastab mitmemõõtmelise järjendi, kus iga alamkaust on omakorda esitatud järjendina ja failid on esitatud vastavas järjendis olevate sõnedena. Kui meil on näiteks selline kataloog:

Muusika
- Eesti musa
  
  kaelakee_hääl.mp3
  
  Bemmi kummid.mp3
- miami_vice_theme.mp3

siis funktsioon peaks tagastama sellise järjendi:

[['kaelakee_hääl.mp3', 'Bemmi kummid.mp3'], 'miami_vice_theme.mp3']

2. Arvamismäng¶

Realiseeri 3. peatükis tutvustatud arvamismäng kasutades tsüklite asemel rekursiooni. Programm peaks pidama arvet arvamiste arvu üle ja lõpetama töö, kui kasutaja on juba n korda ebaõnnestunult arvanud.

3. Fraktal¶

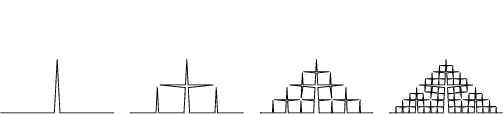
Järgneval pildid on fraktali tasemed 1, 2, 3 ja 4:

Kirjuta funktsioon, mis võtab argumendiks joonepikkuse ja taseme numbri ning joonistab kilpkonnaga vastava taseme fraktali.

Vihje

Seda ülesannet on mugav lahendada kahe funktsiooniga, kus mitterekursiivne põhifunktsioon kasutab rekursiivset abifunktsiooni.

Vihje

Alusta veidi lihtsamast fraktalist:

Selleks, et joonistada lihtsustatud fraktali tase n, tuleb:

joonistada fraktal tasemega n-1;
pöörata (veidi vähem, kui 90 kraadi);
joonistada fraktal tasemega n-1;
teha järsk pööre tagasi;
joonistada fraktal tasemega n-1;
pöörata;
joonistada fraktal tasemega n-1.

Erijuht (baas) on tase 0, kus tuleb joonistada lihtsalt kriips

4. Kuulujutt ver 2¶

Lahenda ülalpool toodud kuulujutu ülesandest ümberpööratud variant.

Antud on linnakese elanike arv n. Leida, mitme tunni pärast teavad kuulujuttu kõik selle linnakese elanikud.

5. Vokaalide eemaldamine¶

Kirjuta rekursiivne funktsioon konsonandid, mis võtab argumendiks sõne ja tagastab sellest sõnest uue variandi, kus kõik vokaalid on eemaldatud, nt konsonandid("kapitalist") peaks tagastama sõne "kptlst". Ülesanne tuleks lahendada ilma tsükleid kasutamata.

Vihje

Tuleta meelde ülalpool esitatud näitefunktsiooni loenda. Seal koguti rekursiivsete väljakutsete tulemused kokku üheks täisarvuks. Siin on vaja korjata tulemused kokku üheks sõneks.

6. Tagurpidi¶

Kirjuta rekursiivne funktsioon tagurpidi, mis võtab argumendiks sõne ja tagastab selle sümbolid uue sõnena vastupidises järjestuses. Nt tagurpidi("stressed") peaks tagastama sõne "desserts". Ülesanne tuleks lahendada ilma tsükleid kasutamata. NB! See funktsioon peaks töötama ka tühja sõne puhul!

Vihje

Tühja sõne puhul on vastus lihtne. Pikemate sõnede puhul võib küsida ümberpööratud versiooni sõne sabast (st esimesele sümbolile järgnevad sümbolid) ja kombineerida (liita) see sõne päisega (st esimese sümboliga).

7. Efektiivsem Fibonacci¶

Ülalpool toodud definitsioon Fibonacci arvude leidmiseks pole optimaalne, sest samu väärtusi peab arvutama mitu korda ning programmi tööaeg kasvab eksponentsiaalselt. Kirjuta funktsioon ümber selliselt, et sama argumendiga väljakutset ei toimuks mitu korda.

Vihje

Üks võimalus selle probleemi lahendamiseks on jätta iga väljaarvutatud Fibonacci arv kusagile meelde. Kui funktsioonilt küsitakse mingit Fibonacci arvu, siis tuleks kõigepealt vaadata, kas vastus on juba eelnevalt välja arvutatud. Võrdle esialgse ja uue funktsiooni töökiirust 40. Fibonacci arvu leidmisel.

Vihje

Alternatiivne võimalus.

Tee abifunktsioon, kus on ainult üks rekursiivne väljakutse, mis tagastab 2 väärtust, st abifunktsiooni ülesanne pole mitte mitte ühe, vaid kahe järjestikuse Fibonacci arvu leidmine.

def fib(n):
    return abi_fib(n)[0]

def abi_fib(n):
    ...
    ...
    return [..., ...]

8. Projecteuler.net¶

Lahenda rekursiooni abil järgmine ülesanne: http://projecteuler.net/index.php?section=problems&id=15.

Vihje

Iga kord, kui sa teed ühe sammu alla või paremale, on su ruudustik (ja probleem) kohe natuke väiksem.
Baasjuhtumina võib käsitleda situatsiooni, kus ruudustiku kõrgus või laius on 0.

9. Sugupuu¶

Antud on fail sugupuu.txt sugulussidemetega (igal real on inimese nimi, koolon ning tema isa ja ema nimed).

Loe esmalt andmed Pythoni sõnastikku (võtmeks inimese nimi, väärtuseks kaheelemendiline järjend tema isa ja ema nimedega).

Kirjuta rekursiivne funktsioon on_eellane, mis võtab argumentideks kahe inimese nimed ja sugupuu sõnastiku ning tagastab True, kui esimene inimene on teise eellane (st isa või vanaema või vanaisa ema jne), vastasel juhul False.

Vihje

A on B eellane, kui ta on B ema/isa või kui ta on B ema/isa eellane.

10. Rekursiivse listi läbimine¶

Kirjuta funktsioon rek_abs, mis võtab argumentideks listi, mille elementideks võivad olla arvud ja/või listid. Igas alamlistis on jällegi arvud ja/või listid jne. Funktsioon peab tagastama uue sama kujuga andmestruktuuri, kus kõik arvud on asendatud nende absoluutväärtusega. Argumendiks antud listi ega ühtegi alamlisti muuta ei tohi.

Näide:

>>> rek_abs([2,-6, [8,-12,-12, [4, [-6], -3]], 7, [3.55, -3.55]])
[2, 6, [8, 12, 12, [4, [6], 3]], 7, [3.55, 3.55]]
>>> rek_abs([])
[]

Vihje

>>> isinstance([1,2,3], list)
True
>>> isinstance(435, list)
False

Lisalugemine¶

Rekursioon, müstika, huumor¶

Mõned viited rekursiooniga seotud koomiksitele, piltidele, mõistetele:

Mitmetes programmeerimiskeelte õpikutes on terminoloogia osas taoline fragment:

Terminid

rekursioon: vt. rekursioon

Öeldakse veel, et rekursiooni mõistmiseks tuleb rekursiooni mõista.

Aritmeetilise avaldise väärtustaja¶

Märkus

See näide demonstreerib ühte ilusat rekursiivset algoritmi. Nagu rekursiivsete algoritmide puhul tavaline, võib see alguses aju sõlme keerata – varu endale selle teema läbitöötamiseks piisavalt aega!

Ülesanne: kirjutada funktsioon, mis võtab argumendiks sõne kujul aritmeetilise avaldise ja tagastab selle väärtuse. Avaldis võib sisaldada arve, aritmeetilisi operatsioone (+, -, *, /) ning sulge (mitmel tasemel). Seal, kus sulge pole kasutatud, tuleb arvestada tavalise tehete järjekorraga.

(Lihtsuse mõttes võime esialgu eeldada, et kõik avaldise komponendid on üksteisest tühikutega eraldatud, nt 3 * ( -4 / 3.5 + ( 3 - 2 ) ) - 6 – sedasi on lihtsam avaldist komponentideks jagada.)

Märkus

Enne edasi lugemist mõtle, kuidas sa sellise ülesande lahendaksid. Katseta! Milline ülesande aspekt valmistab kõige rohkem probleeme?

Astu samm tagasi ja mõtle, milline võib olla aritmeetilise avaldise struktuur.

Alljärgnevalt on toodud mõned näited erineva struktuuriga avaldistest:

3 — arv;
3 + 2 — liitmine, kus argumendid on arvud;
3 * 10 + 2 * 10 — liitmine, kus argumendid on korrutised;
3 - 2 - 6 — loetakse ( 3 - 2 ) - 6; s.o lahutamine, kus vasak argument on lahutamine (3 - 2) ja parem argument on arv (6);
3 + 2 * 3 — loetakse 3 + ( 2 * 3 ); s.o liitmine, kus vasak argument on arv ja parem argument on korrutamine;
( 3 + 2 ) — sulgudes olev avaldis;
( 3 + 2 ) * 3 — korrutamine, kus vasak argument on sulgudes olev avaldis ja parem argument on arv.

Viimases kahes näites kasutasime avaldise struktuuri kirjelduses mõistet avaldis – st me kirjeldasime avaldise olemust rekursiivselt.

Enne edasi minemist defineerime abimõisted erinevatel kujudel avaldiste tähistamiseks.

faktor – arv või sulgudes olev avaldis, nt 3 või ( 2 * 3 + ( 4 / 6 ) ).
term – faktor või korrutis/jagatis, nt 3, ( 2 * 3 + ( 4 / 6 ) ) või 2 * ( 3 + 4 ). Pane tähele, et korrutise/jagatise vasak argument võib olla term aga parem argument on faktor (mõtle 8 / 2 / 2 struktuuri peale).
avaldis – term või liitmine/lahutamine. Liitmise/lahutamise vasak argument võib olla avaldis, aga parem argument on term.

Paneme samad mõisted kirja ka spetsiaalses notatsioonis, mida kasutatakse grammatikate esitamiseks (| võib lugeda kui sõna või):

avaldis  :  term    |  avaldis ('+' | '-') term
term     :  faktor  |  term    ('*' | '/') faktor
faktor   :  arv | '(' avaldis ')'

Avaldise väärtustamise plaan:

Mugavuse mõttes teisendame sõne märkide järjendiks nii, et iga märk on kas mingi operaator, arv või sulg. Edasine töö toimub märkide järjendi põhjal.
Loome iga avaldise tüübi jaoks eraldi funktsiooni (loe_avaldis, loe_term, loe_faktor), mis võtab argumendiks märkide järjendi, loeb järjendi lõpust selle jupi, mida ta tunneb (vastavalt avaldise, termi või faktori) ning tagastab selle jupi väärtuse. Loetud jupp eemaldatakse märkide järjendist – seega muutub järjend igal etapil järjest lühemaks.
Märkide järjendi lühendamiseks kasutame meetodit pop, mis eemaldab ja tagastab järjendi viimase elemendi.
Kui kõik läheb ilusti, siis funktsiooni loe_avaldis töö lõpus on märkide järjend muutunud tühjaks järjendiks ja saadud vastus ongi avaldise väärtus.

Selle plaani põhjal on kirjutatud järgnev programm, mis toetub rekursiivsetele funktsioonidele:

def väärtusta_avaldis(avaldis):
    # tühikuid nõudsime selleks, et osadeks jaotamine oleks lihtsam
    märgid = avaldis.split()
    tulemus = loe_avaldis(märgid)
    if märgid != []:
        print("Mingi jama, allesjäänud märgid:", märgid)
    return tulemus

def loe_avaldis(märgid):
    # nagu avaldise grammatika ütleb, on avaldise lõpus alati term
    parem_argument = loe_term(märgid)

    # kui enne termi on operaator (+ või -), siis enne operaatorit peab olema avaldis
    if märgid != [] and märgid[-1] in ['+', '-']:
        operaator = märgid.pop() # pop tagastab ja eemaldab listi viimase elemendi
        vasak_argument = loe_avaldis(märgid)
        if operaator == '+':
            return vasak_argument + parem_argument
        else:
            return vasak_argument - parem_argument

    # kui liitmist/lahutamist pole, siis järelikult on tegemist
    # avaldise lihtsa variandiga (e lihtsalt termiga)
    else:
        return parem_argument

def loe_term(märgid):
    # selle funktsiooni ülesehitus on eelmisega analoogne
    parem_argument = loe_faktor(märgid)

    if märgid != [] and märgid[-1] in ['*', '/']:
        operaator = märgid.pop()
        vasak_argument = loe_term(märgid)
        if operaator == '*':
            return vasak_argument * parem_argument
        else:
            return vasak_argument / parem_argument
    else:
        return parem_argument

def loe_faktor(märgid):
    märk = märgid.pop()

    if märk == ')': # tegemist on sulgudes oleva avaldisega
        tulemus = loe_avaldis(märgid)
        # nüüd on eeldatavasti viimaseks sümboliks '(', "loeme" ka selle ära
        sulg = märgid.pop()
        if sulg != '(':
            print("Mingi jama!")
        return tulemus
    else:
        # pop-itud märk peab olema arv
        return float(märk)

print(väärtusta_avaldis("3"))
print(väärtusta_avaldis("( 3 )"))
print(väärtusta_avaldis("3 * ( -4 / 3.5 + ( 3 - 2 ) ) - 6"))
print(väärtusta_avaldis("3 * 3"))
print(väärtusta_avaldis("( 3 + 3 * 4 )"))
print(väärtusta_avaldis("( 3 + 3 ) * 4"))
print(väärtusta_avaldis("1 + 1 + 1 + 1"))
print(väärtusta_avaldis("2 * 2 * 2 * 2"))

Märkus

Selles programmis on lisaks otsesele rekursioonile mängus ka kaudne rekursioon – nt funktsioon loe_faktor ei kutsu küll otseselt iseend välja, kuid ta võib kutsuda välja funktsiooni loe_avaldis, mis võib kutsuda välja loe_term-i, mis võib kutsuda välja loe_faktor-i.

Küsimus

Miks ei võiks me alustada märkide järjendi läbimist algusest?

Labürintide genereerimine¶

Üks huvitav näide rekursiooni kasutamisest on juhuslike labürintide genereerimine.

Kujutame ette, et meil on suur plokk betooni, kuhu me hakkame uuristama ploki külgedega paralleelseid ja aeg-ajalt täisnurga all pööravaid, mõnikord ka hargnevaid käike. Igal sammul on meil mitu võimalust, kuhupoole edasi uuristada. Üks võimalus probleemile läheneda, on uuristada üks juhuslik labürint otse ette, teine labürint vasakule ja kolmas paremale, aga selle, millisest alam-labürindist me alustame, valime juhuslikult. Selleks, et labürint ei tuleks triviaalne, jälgime, et me ei puuriks läbi seda seina, mille taga vahetult on juba üks käik uuristatud – see tingimus tagab, et iga järgmise alam-labürindi võimalik ala on järjest väiksem (ilmselt märkad siin juba viidet rekursiooni põhimõtetele).

Selle algoritmi kohta võid täpsemalt uurida vastavast Wikipedia artiklist (http://en.wikipedia.org/wiki/Maze_generation_algorithm) või laadida alla ühe näiteprogrammi (mazes.py), mis kasutab Pygame nimelist Pythoni lisateeki (tuleb eraldi installeerida, saadaval aadressilt http://pygame.org).